线性代数中的可视化教学

线性代数中的可视化教学

赵东霞, 张乐, 姚林红

中北大学数学学院，山西太原

摘要：线性代数课程具有抽象、知识点细碎、且环环相扣、错综复杂的特点，教师如何设计教学过程是值得关注的一个重要课题.本文致力于将线性代数中抽象的定义、定理、习题等进行可视化设计的探索，符合新工科教学改革中提升应用性、提高课堂教学效果、调动学生学习兴趣、培养应用型人才的目的。

1 引言

线性代数课程的特点是公式多，符号繁，内容抽象，知识点细碎，记忆量大且容易混淆的地方多，不同章节知识点间联系紧密：既相互推导，又前后印证。因此，这是一门学的不好就显得特别难的科目[1]。由于工科生普遍具有形象思维发达、抽象能力和逻辑推理能力薄弱的特点，导致教师在教学中发现：学生内心对这门课程比较排斥，学习积极性不高[2]，尤其在教授部分知识点时甚至有种“ 对牛弹琴”、师生之间隔着一堵墙的无力感。那么，如何提高学生的学习效率和能力，提高学生学习的积极性是每个教师都值得思考和研究的问题， 其中借助现代多媒体辅助教学技术对课程进行灵活教学是一种切实可行的解决方案[3]。基于STEM教育理念，以矩阵及矩阵计算为例且融合数学图像处理的基础技术设计线性代数可视化教学已有一些成果[4].文献[5]利用Matlab对方程组进行求解且画出了二元齐次非线性方程组的可视化图像。文献[6]中基于微课的翻转课堂这种教学模式极大地调动了学生学习线性代数的热情和积极性，也取得了不错的教学效果。因此，在线性代数的教学中运用数学软件以及实际生活背景直观化地进行教学是迫切需要探索的。基于此，中北大学数学学院尝试改革线性代数传统教学方法，进行教学的“可视化”探索与研究，本文将可视化教学全面地应用在线性代数概念、定理、习题等的教学中。

所谓可视化教学旨在利用可视易懂的方式诠释基础知识，利用丰富的图例展示各种抽象的数学概念、定理和证明思路，形成能够直接作用于人的感官的知识外在表现形式，促使教学效果达最优[7]。一图胜千字，图是最直观的语言，易读、易懂、且易记，借助图像把看不见的思维过程呈现出来，将引导学生进入会学、乐学的良性循环[8]。知识可视化工具不仅包括概念图、流程关系图、表格、框图、思维导图，还有Mathematica、Matlab等数学软件图像功能，它可以直观地展示数学之美，加深学生对知识点的理解，同时培养学生的空间想象力， 锻炼学生的动手能力，提高学生的学习主动性和积极性，增强课堂的趣味性，激发学生的探索欲，是达到《国家中长期教育改革和发展规划纲要》明确提出的“培养本领过硬的高素质专门人才和拔尖创新人才”的一种有效途径。

化抽象为直观，将知识点生动形象地展现在学生面前，MATLAB数学软件即为实现这一目标的强有力工具[9]。MATLAB是matrix与laboratory两个词的组合，意为矩阵工厂或矩阵实验室，软件主要面对科学计算、可视化以及交互式程序设计的高科技计算环境.以矩阵作为基本编程单元，提供了各种矩阵的运算，有较强的数据可视化功能[10]。因此， 我们可以借助MATLAB的“可视化”效果使线性代数课程教学难度降低、教学内容变得鲜活生动， 还可以通过一种直观语言的方式理解线性代数中的内容，使学生对线性代数的知识有一个更直观的体会，提高学习兴趣，达到融会贯通，全面把握知识点间的联系，灵活运用的学习效果。

2 概念可视化

线性代数课程中概念多且非常的抽象，传统的教学方式就是教师直接讲解，学生们只能从代数的角度对概念有一个非常浅显的理解，按部就班地进行运算。如果我们能够借助Matlab中强大的可视化功能将数据可视化，有一个直观的展示，那么对线性代数知识的理解也就没有那么遥不可及了。

案例1 数形结合思想与正定二次型

传统教学在给出正定二次型的定义后，直接罗列了各种判定方法，虽然这些判定方法本身并不难，但学生常有的疑问是“为什么要定义正定二次型？有什么特殊的含义呢？”实际上，二次型即为二次齐次函数，对于二元二次型，和高等数学里面的二元函数是相通的，我们借助于MATLAB数学软件中ezmesh函数可将二元二次型的函数图像在三维空间直角坐标系中呈现出来，使同学们认识到二元正定二次型即为一张位于xoy面上方的曲面（如图1），如果二元二次型的函数图象既有位于xoy面上方的部分，也有位于xoy面下方的部分，那么一定不是正定二次型（如图2所示）。因此，MATLAB 数学软件作为媒介，将数形结合思想应用在线性代数的教学中，使抽象定义可视化，极大地提高了教学效果，也给线性代数的课堂教学带来了生机和活力，使学生更容易理解和接受知识。

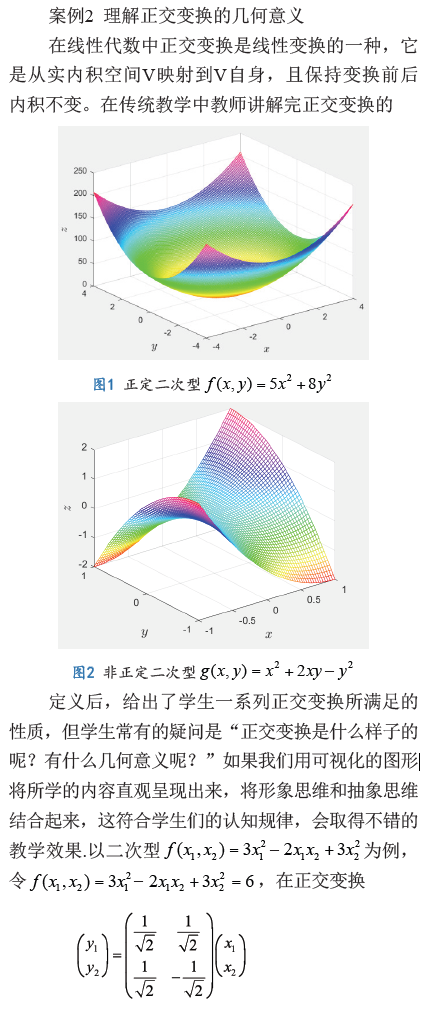
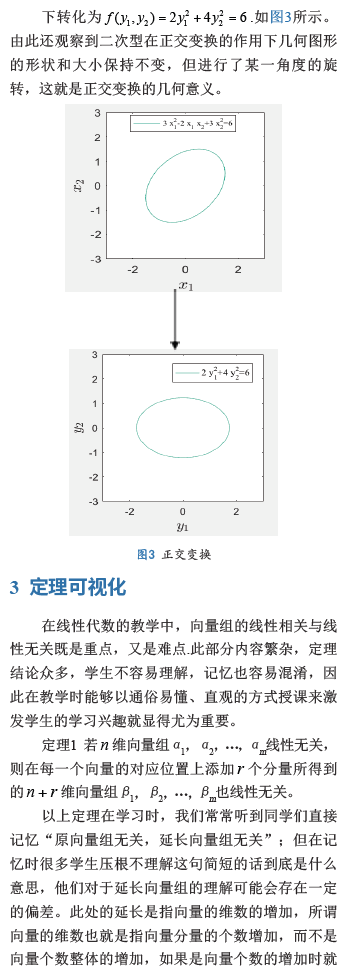
图6和图7反映的是线性方程组(2)无解和线性方程组(3)有无穷多组解的情形。

通过Matlab软件强大的可视化功能，让学生们更加直观的理解线性代数习题的知识点，并且遇到习题中一些高阶的复杂计算时，依然可以采用以上的方法，消除了学生们的畏惧心理，增强学习线性代数的积极性。

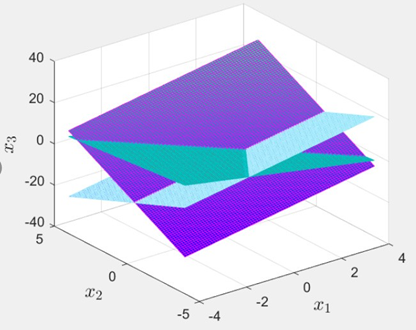
图5 线性方程组(1)有唯一解

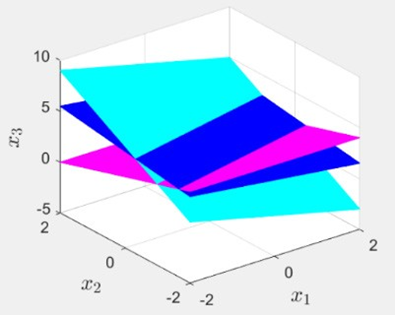
图6 线性方程组(2)无解

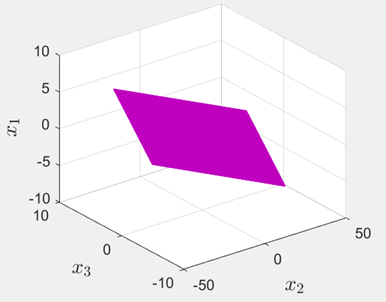
图7 线性方程组(3)有无穷多组解

5 结论

线性代数是各大高校理、工、文、经、管等本科相关专业大学生的一门综合必修数学基础理论课，该课程是从具体概念抽象出来的公理化方法、严格的逻辑推证、巧妙的归纳综合，体现了几何观念与代数方法之间的联系，是数形结合思想的完美呈现，对于强化数学训练、培养数学思维、增强创新能力是非常有用的。本文将可视化教学全面地应用在线性代数概念、定理、习题等教学中，旨在帮助学生直观理解和掌握核心知识，激发学生的学习兴趣和积极性。

致谢

本文由山西省高等学校教学改革创新项目(项目编号：J20240885) 资助。