初中生数学逻辑推理能力调查研究

初中生数学逻辑推理能力调查研究

何依诺，俞宏毓

南京信息工程大学，江苏南京

摘要：逻辑推理是数学学科核心素养之一，培养学生的数学逻辑推理能力对于他们的学业成绩、思维能力、问题解决和全面发展都至关重要。编制数学逻辑推理能力测试卷，分析初中生数学逻辑推理能力的现状以及各维度在性别、年级的差异，了解学生数学逻辑推理能力的发展特点，结果如下：初中生数学逻辑推理能力整体处于中等水平，且学生之间能力差异较大；五个维度中简单推理能力最强，合情推理最差；初中生数学逻辑推理能力及其各维度在性别上无显著差异；除了选言推理外，逻辑推理总测验及其他各维度在年级上均存在显著差异；初中生数学逻辑推理能力整体上在三年中稳步发展，且在八年级发展更为快速。

1 引言

数学逻辑推理能力在国际上被广泛认可为一项重要的学生能力，我国积极应对21世纪挑战和国际教育竞争，不断推进教育改革。新修订的《义务教育数学课程标准（2022年版）》正式将义务教育阶段的数学核心素养写进课程标准之中，并提出培养学生“会用数学的思维思考现实世界”^[1]。数学逻辑推理能力是数学思维的核心组成部分，是培养学生的创新思维、问题解决能力和批判性思维能力的基础，在数学逻辑推理的学习过程中，学生可以逐步形成严谨缜密的逻辑思维，提升分析问题和解决问题的能力，学会用数学的思维思考世界，成长为有良好逻辑推理素养的21世纪人才。

国际上的教育评估项目对学生的数学能力和逻辑推理能力进行了广泛的调查和比较。如PISA2022数学素养测试框架分为三个领域：数学内容、数学过程和数学情境，其中数学过程评估学生使用数学推理和应用数学解决问题的能力^[2]。2023年TIMSS测试初中数学评价框架的认知维度分为“知道”、“应用”、“推理”三个领域，其中，推理领域包括“分析”“整合”“概括”“论证”四个层级^[3]。SOLO分类评价理论由香港大学教育心理学教授Biggs创立，他将学生学习结果由低到高划为五个水平：前结构层次、单线结构层次、多线结构层次、结构层次、拓展层次^[4]。这些研究提供了跨国比较的数据，揭示了不同国家和地区学生在数学能力方面的差异和趋势，但其只是在对能力、素养的测评中强调了逻辑推理的重要性，并没有针对逻辑推理提出测评框架。

国内一些学者通过编制各类数学能力评价工具，对初中生的数学逻辑推理能力进行评估。如孙婷从内容、结构和过程三个维度构建学生数学推理论证能力的三维“金字塔式”测评框架^[5]；蒋艳改编PISA测试题，设计出针对优等生的调查试题，并应用SOLO分类理论评价学生思维水平^[6]；潘宇基于SOLO分类理论与演绎推理自身分类，建立评价量表，了解贵州民族地区学生数学演绎推理能力情况^[7]；袁柳芳以“尤西斯金测验”以及其自编的“形式逻辑推理层次测验”为工具，调查八年级学生几何推理能力^[8]；卢雪栋利用R0T测验量表了解学生空间推理能力^[9]；严卿提出了测量初中生逻辑推理能力的框架，并编制了相应的测验题，该测试题将数学逻辑推理分为简单推理、选言推理、命题演算、假言推理和合情推理五个维度，考察学生逻辑推理能力的发展水平^[10]。一些研究则关注于开展针对逻辑推理能力的教学干预研究，通过设计和实施特定的教学活动和策略，试图提升学生的逻辑推理能力。如周雪兵通过分析具体例题，提出“充分发挥学生的想象力、放手让学生去体验、引导学生掌握逻辑推理的方法”的教学建议^[11]。总体来看，国内对于数学逻辑推理能力的测评研究较为零散，且部分结论存在争议，仍需更为系统、深入的研究。

结合对相关研究的分析，研究者旨在通过研究初中生数学逻辑推理能力现状、差异以及发展特点，帮助教育工作者改进教学，对学生进行能力评估与综合能力培养。

2 研究设计

2.1 研究对象

本研究选取南京一中考升学率为中等水平的初中七、八、九三个年级共349名学生进行测试调查。剔除无效样本1项，得到样本348人，其中，七年级142人，八年级67人，九年级139人；剔除未填性别样本后，七年级女生66人，男生68人，八年级女生28人，男生35人，九年级女生57人，男生73人。

2.2 研究工具

2.2.1 测试卷的编制

本研究测试卷改编严卿在《初中生逻辑推理的测验研究》中编制的测试卷^[10]，将初中生数学逻辑推理能力划分为简单推理、选言推理、假言推理、命题演算以及合情推理五个维度。考虑到原测试卷只涉及到三段论的第一格（t3、t4），具有局限性，本研究将测试卷t3改编为三段论第三格；在测试卷结构方面，本研究增加一道假言推理题，减少一道合情推理测试题；另外，结合初中生竞赛题、中考题，对第二、四、六、十二、十三、十五、十八、十九、二十、二十二题进行改编；改编后，本研究测试卷共22题，题项分布见表1。

表1.测试卷题项分布表

测试题维度	题号
简单推理	1、2、3、4
选言推理	5、6、7、8
假言推理	9、10、11、12
命题演算	13、14、15、16
合情推理	17、18、19、20、21、22

2.2.2 测试卷信度与效度

信度可以衡量测量工具的可靠性、一致性或稳定性，Cronbach's alpha系数越接近1，测试卷具有越高的内部一致性和可靠性。本研究测试卷Cronbach’s α系数为0.725，表明测试卷具有良好的信度。

表2.信度检验表

Cronbach's α系数	标准化Cronbach's α系数	项数
0.715	0.725	25

效度指测试卷能否准确、完整地反映被测试的现象。本研究测试卷KMO值为0.717，显著性p值<0.001，效度较高，表明测试卷设计较合理。

表3.效度检验表

KMO值		0.717
Bartlett球形度检验	近似卡方	1031.399
	df	300
	P	0.000***

注：***代表1%的显著性水平

2.2.3 测试卷难度与区分度

难度反映测试卷的难易程度。用P表示难度，其计算公式为P=平均值/满分值，P越大则试题越简单。根据难度计算公式得到本测试卷P值为0.47，试题难度适宜。

区分度指试题对被测试者情况的分辨能力。将学生测试成绩从高到低排序，计算前27%学生的平均分X_H，后27%学生的平均分X_L，试题满分W，则区分度D=（X_H-X_L）/W，得到各题区分度见表4。大多数题项区分度在0.4以上，区分度很好，部分题项区分度在0.3–0.4之间，区分度较好。

表4.测试卷区分度情况表

1	2	3	4	5	6	7	8
0.564	0.468	0.437	0.702	0.468	0.564	0.314	0.517
9	10	11	12	13	14	15	16
0.671	0.681	0.138	0.713	0.532	0.607	0.734	0.649
17	18	19	20	21	22
0.446	0.479	0.585	0.277	0.383	0.405

3 研究结果

3.1 初中生数学逻辑推理能力概况

利用SPSS27.0软件对测试卷进行描述性统计分析，总测验结果见表5。测试卷总分44分，学生平均分20.753，中位数20，众数19，单题平均分0.943，样本整体数学逻辑推理能力处于中等水平。分数最高42，最低3，极差39，标准差7.803，样本内部逻辑推理能力有一定的分散情况。峰度−0.474，表明各个分数段均有分布，偏度0.272，表明分数分布高峰向较低分偏移。

表5.总测验描述性统计

	样本量	最大值	最小值	平均值	标准差	中位数	峰度	偏度	单题平均分
总测验	348	42	3	20.753	7.803	20	−0.474	0.272	0.943

数学逻辑推理各维度描述性统计结果见表6，五个维度均有学生获得满分和零分，简单推理单题平均分最高，为1.28分，选言推理次之，平均分为0.994，假言推理和命题演算平均分相差不大，分别为0.901和0.923，合情推理单题均分最低，为0.675分。

五个维度样本峰度均小于0，分数分布较平缓，各个分数段都有分布。其中，命题演算峰度的绝对值与0相差最大，表明该维度下学生分数极端值较多，合情推理峰度为−0.161，相较于其他维度分数极端值较少。

简单推理与选言推理样本分数偏度小于0，呈左偏态分布，分数分布高峰向较高分偏移，假言推理、命题演算与合情推理偏度大于0，呈右偏态分布，分数分布高峰向低分段偏移，与其平均分较低相符合。

数学逻辑推理的五个维度变异程度均较高，其中合情推理样本分数变异程度最高，为0.664，表明该维度下分数的离散程度最高，简单推理变异系数最低，为0.417，该维度下分数变异程度最小。

表6.逻辑推理各维度描述性统计

维度	最大值	最小值	平均值	中位数	峰度	偏度	满分	单题 平均分	变异系数
简单推理	8	0	5.115	6	−0.33	−0.424	8	1.28	0.417
选言推理	8	0	3.974	4	−0.757	−0.021	8	0.994	0.493
假言推理	8	0	3.603	4	−0.688	0.055	8	0.901	0.607
命题演算	8	0	3.695	4	−0.985	0.11	8	0.923	0.657
合情推理	12	0	4.052	4	−0.161	0.53	12	0.675	0.664

3.2 初中生数学逻辑推理能力的差异研究

3.2.1 数学逻辑推理能力的性别差异

剔除未填写性别的样本，剩余327个样本。为探究数学逻辑推理能力在性别上是否存在差异，分别以总分、简单推理、选言推理、假言推理、命题演算、合情推理得分为因变量，以性别为影响因子，对样本进行方差分析。描述性统计结果见表7。

表7.男女逻辑推理得分描述性统计

维度	男M（SD）	女M（SD）
总测验	20.466（8.112）	21.325（7.554）
简单推理	4.977（2.073）	5.285（2.146）
选言推理	3.915（1.977）	4.06（1.974）
假言推理	3.511（2.225）	3.772（2.155）
命题演算	3.795（2.457）	3.642（2.434）
合情推理	3.977（2.844）	4.265（2.599）

方差齐性检验的结果显示，总成绩显著性p值为0.333，简单推理显著性p值为0.506，选言推理显著性p值为0.748，假言推理显著性p值为0.368，命题演算显著性p值为0.883，合情推理显著性p值为0.351，水平上均不呈现显著性，不能拒绝原假设，因此数据满足方差齐性。

由于总测验及其各维度均满足方差齐性，故采用独立样本T检验，总测验、简单推理、选言推理、假言推理、命题演算、合情推理显著性结果p值分别为0.325、0.189、0.059、0.387、0.573、0.344，因此统计结果不显著，说明男、女在总测验及其各维度上均不存在显著差异;且其差异幅度Cohen's d均小于0.2，差异幅度非常小（0.20，0.50和0.80分别对应小、中、大临界点）。

3.2.2 数学逻辑推理能力的年级差异

为探究数学逻辑推理能力在年级上是否存在差异，分别以总分、简单推理、选言推理、假言推理、命题演算、合情推理得分为因变量，以年级为影响因子，对样本进行方差分析。描述性统计结果见表8。

表8.逻辑推理各年级得分描述性统计

维度	七年级M（SD）	八年级M（SD）	九年级M（SD）
总测验	18.254（6.885）	19.81（6.146）	23.888（8.45）
简单推理	4.746（2.805）	4.836（1.814）	5.626（2.227）
选言推理	3.655（1.872）	4.104（1.884）	4.237（2.049）
假言推理	2.803（1.965）	3.433（1.901）	4.504（2.208）
命题演算	3.31（2.394）	3.403（2.283）	4.23（2.445）
合情推理	3.69（2.569）	3.463（2.351）	4.705（2.847）

方差齐性检验的结果显示，总测验显著性p值为0.000***，水平上呈现显著性，拒绝原假设，因此数据不满足方差齐性。简单推理显著性p值为0.144，选言推理显著性p值为0.613，假言推理显著性p值为0.445，命题演算显著性p值为0.517，合情推理显著性p值为0.233，水平上均不呈现显著性，不能拒绝原假设，因此数据满足方差齐性。

对于总测验，由于不满足方差齐性，采用Welch's 方差检验，方差分析结果p值为0.000***≤0.05，因此统计结果显著，说明不同的年级在总成绩上存在显著差异。对于简单推理、选言推理、假言推理、命题演算、合情推理，由于满足方差齐性，采用单样本方差检验，方差分析结果p值分别为0.002***、0.060*、0.000***、0.005***、0.001***，其中简单推理、假言推理、命题演算、合情推理p值均小于0.05，统计结果显著，说明不同年级之间存在显著差异；而选言推理方差分析结果p值0.060*>0.05，因此统计结果不显著，不同的年级在选言推理上不存在显著差异。

当单因素方差分析结果呈现出显著性差异，可以进一步分析差异幅度。偏Eta方（η²值）介于0~1之间，该值越大说明差异幅度越大，其差异幅度小、中、大的区分临界点分别是0.01，0.06和0.14；Cohen's f值表示效应量大小，效应量小、中、大的区分临界点分别是0.1、0.25和0.40。效应量化分析的结果显示：基于总测验，η²值为0.069，说明数据的差异有6.9%是来源于不同组别间的差异，Cohen’s f值为0.273，说明数据的效应量化的差异程度为中等程度差异；基于简单推理，η²值为0.039，Cohen’s f值为0.201，差异程度为小程度差异；基于假言推理，Eta方η²值为0.138， Cohen’s f值为0.4，差异程度为大程度差异；基于命题演算，η²值为0.033， Cohen’s f值为0.184，差异程度为小程度差异；基于合情推理，Eta方η²值为0.039，Cohen’s f值为0.202，差异程度为小程度差异。

3.3 初中生数学逻辑推理能力发展特点

由差异分析可知，简单推理、假言推理、命题演算、合情推理在年级上均存在显著差异，选择LSD方法进行事后多重比较，结果见表9，简单推理九年级得分显著高于八年级，假言推理八年级得分显著高于七年级且九年级得分显著高于八年级，命题演算九年级得分显著高于八年级，合情推理九年级得分显著高于八年级。

表9.各维度得分事后多重比较

维度	(I)名称	(J)名称	(I)平均值	(J)平均值	差值(I-J)	P
简单推理	九年级	八年级	5.626	4.836	0.79	0.012**
假言推理	七年级	八年级	2.803	3.433	−0.63	0.039**
	九年级	八年级	4.504	3.433	1.071	0.001***
命题演算	九年级	八年级	4.23	3.403	0.827	0.021**
合情推理	九年级	八年级	4.705	3.463	1.242	0.002***

注： ***、**分别代表1%、5%的显著性水平

数学逻辑推理各维度在各年级的得分率见表10，总测验、简单推理、假言推理、命题演算、合情推理在七年级和八年级的得分率均小于三个年级总的人均得分率，九年级的人均得分率高于总的人均得分率，且八年级至九年级得分率的增长幅度大于七年级至八年级；选言推理八年级和九年级得分率高于三个年级总的人均得分率，且七年级至八年级得分率增长幅度大于八年级至九年级。

表10.逻辑推理各年级得分率

维度	七年级	八年级	九年级	总计
总测验	41.49%	45.02%	54.29%	47.17%
简单推理	59.33%	60.45%	70.33%	63.94%
选言推理	45.69%	51.30%	52.96%	49.68%
假言推理	35.04%	42.91%	56.30%	45.04%
命题演算	41.38%	42.54%	52.88%	46.19%
合情推理	30.75%	28.86%	39.21%	33.77%

结合数学逻辑推理各维度得分随年级增长的变化折线图可知，初中生简单推理和命题演算在八年级至九年级的发展幅度大于七年级至八年级，假言推理能力在七年级至九年级稳步提升，选言推理在七年级至九年级变化幅度较小，而合情推理在七年级至八年级有一个小幅下降，在八年级至九年级迅速发展。

 

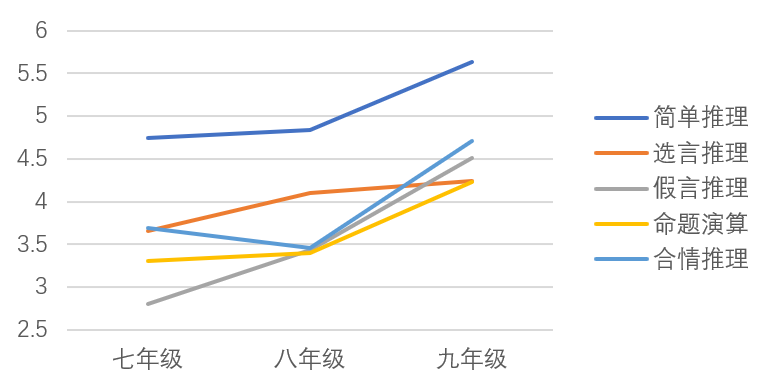
图1.逻辑推理各维度得分折线图

4 研究结论

（1）初中生数学逻辑推理能力概况

初中生数学逻辑推理能力整体处于中等水平，且学生之间能力差异较大；初中生数学逻辑推理能力五个维度中简单推理能力最强，选言推理次之，合情推理最差。

（2）初中生数学逻辑推理能力在性别、年级上的差异

初中生数学逻辑推理能力及其各维度在性别上无显著差异。除了选言推理外，逻辑推理总测验及其他各维度在年级上均存在显著差异，其中简单推理、命题演算、合情推理为小程度差异，总测验为中等程度差异，假言推理为大程度差异。

（3）初中生数学逻辑推理能力发展特点

初中生数学逻辑推理能力整体上在三年中稳步发展，且八年级发展更为快速。简单推理、命题演算在八年级至九年级的提升幅度大于七年级至八年级，假言推理能力三年中较快速地稳步提升，合情推理在八年级至九年级发展迅速，而选言推理三年之间的变化幅度较小。

附录