Downloads
Download


This work is licensed under a Creative Commons Attribution 4.0 International License.
基于5E教学模式的高中数学建模教学设计——以“轮船渡江”为例
冯晗暄
扬州大学数学科学学院,江苏扬州
摘要:应用5E教学模式对“轮船渡江”案例进行高中数学建模的教学设计,通过阐述引入、探究、解释、精致和评价环节的设计内容与意图,着重培养学生的数学核心素养。
1 引言
“数学建模”作为高中数学课程标准确定的六大核心素养之一,旨在培养学生应用数学知识与数学思想方法解决实际问题的能力,其重要性不言而喻。数学建模需要走进高中课堂,高中数学教师需要在教学中强化学生的建模能力,那么如何有效开展相关教学是目前广大教师面临的新挑战[1]。
5E教学模式由美国生物学课程研究所(BSCS)开发,是基于建构主义理论和概念转变理论,在国内外影响广泛的一种探究式教学模式[2]。5E教学模式共包括5个教学环节,分别为引入( Engagement) 、探究( Exploration) 、解释( Explanation) 、精致( Elaboration) 和评价( Evaluation)。该模式广泛应用于实验教学、概念教学等,但在数学建模教学上的尝试较少,而数学建模本质上就是一种探究性学习,适合运用5E教学模式进行教学。
基于此,本研究以“轮船渡江”为例,尝试基于5E教学模式的基本环节进行数学建模教学设计,同时阐述每个环节的设计内容与意图,以期为教师有效开展数学建模教学,培养学生数学建模核心素养提供参考。
2 教学内容
本次教学的载体为“轮船渡江”案例,该案例是笔者根据“小船渡河”问题启发而来。小船渡河问题是高中物理必修二中关于运动的合成与分解的典型实例,笔者借助小船渡河的例子,结合生活中汽渡渡江的现实情境,设计了寻找渡江时间最短方案的数学建模问题,此处称之为“轮船渡江”问题[3]。
3 教学目标
教学目标采用南师大喻平老师的核心素养水平分析方法制定[4]。具体如下(见表1):
表1. 核心素养水平分析方法制定
|
|
数学建模(水平二) |
数学运算(水平二) |
数学抽象(水平三) |
|
情境与问题 |
能够在轮船渡江的现实情境中,发现问题,提出问题,并转化为数学问题。 |
能够在轮船渡江的现实情境中,根据水平和竖直方向的运动方程,提出运算问题。 |
能够在轮船渡江的现实情境中抽象出数学问题,并用恰当的数学语言予以表达。 |
|
知识与技能 |
能够完成数学建模的一般步骤,建立模型,求解模型,根据问题的实际意义检验结果,完善模型。 |
能够根据提出的运算问题,使用编程软件设计运算程序,解决问题。 |
能够抽象出数学图形,给定参数,结合图形建立模型,解决问题。 |
|
思维与表达 |
能够在实际情境中,经历数学建模的过程,理解数学建模的意义;能够运用数学语言,表述建模过程中的问题以及解决问题的过程和结果。 |
能够在使用编程软件解决问题的过程中,体会程序思想的意义和作用。 |
在现实问题中,能够把握轮船渡江的数学特征,并用数学图形和数学语言予以清晰地呈现与表达。 |
|
交流与反思 |
能够形成研究报告,展示研究成果;能够在交流中发现模型存在的不足并改正。 |
在交流的过程中,能够借助运算结果探讨问题,修正模型。 |
在交流的过程中,能够用建立的数学模型解释更多的应用场景。 |
|
品格价值观 |
理解数学建模的价值和意义,体会数学与生活的联系;培养运用数学解决实际问题的能力,提升学生的思维品质,形成正确的数学价值观。 |
||
4 教学重难点
教学重点:能够建立合理的数学模型并求解;能够初步体验数学建模的全过程;
教学难点:能够对模型不断改进,得到更优化的数学模型;能够完成数学建模的核心环节,掌握数学建模的基本方法和步骤。
5 教学环节及设计意图
5.1 引入
情境:图1是镇江—扬州的渡口,轮船从镇扬汽渡镇江站出发驶往扬州站。
图1.镇江—扬州渡口现实图
教师展示镇江—扬州汽渡口的照片,播放轮船渡江的视频,同时提供关于轮渡的一些基本资料,并提出问题:从镇江到扬州,轮船以何种方案渡江可以使得时间最短,求最短的渡江时间。
学生结合自身的现实体验,进行小组讨论,尝试寻找轮船渡江时间最短的方案。
【设计意图】创设情境引起学生兴趣,是5E教学模式的开始环节。该环节从现实中轮船渡江的情境出发引出数学建模问题,有利于调动学生积极性,引入环节也是数学建模过程的第一步,即如何从社会或者自然现象中抽象出建模的主题。
5.2 探究
问题1:影响轮船渡江时间的因素有哪些?
问题2:这些影响因素中,哪些是主要因素,哪些是次要因素?
主要因素:距离、速度、航行方向;次要因素:轮船质量、材质、水速、风速、天气等。
问题3:为了简化问题,可以弱化一些次要因素,基于此请尝试做出模型假设。
假设轮船是一个质点;假设在航行过程中,风速、降水等天气因素对轮船的影响可忽略不计;等等。
【设计意图】问题1到3是数学建模中的重要环节——模型假设的过程,引导学生做出假设,有助于培养学生的逻辑思维,发展数学建模核心素养。
问题4:尝试画出抽象的数学图形,根据主要影响因素确定相关量,并尝试运用数学语言表达所求问题。
问题5:根据轮船在水平与竖直方向的运动情况,建立合理的数学模型。
相关量:设水速为 ,垂直于岸边的距离为 ,平行于河岸的位移为 ,起点至终点之间的直线距离为 ,船航行的速度为 ,航行方向与河岸平行方向夹角为 ,整个航行时间为 (见图2)。
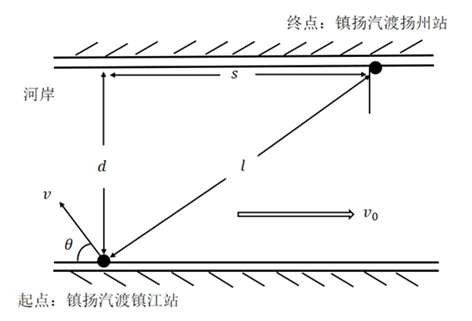
图2.轮船航行示意图
根据水平和竖直方向的运动情况,可得数学模型:
【设计意图】问题4到5是模型建立的过程,该过程可以基本实现教学目标中“数学抽象”水平三的要求,即能够在综合的情境中抽象出数学问题和数学图形,并用数学语言进行表达,有利于培养学生从实际问题中抽象出数学问题的能力,发展学生数学抽象、数学建模的核心素养。
问题6:查阅地图、文献等相关资料,获取所需要的数据信息。
问题7:利用MATLAB软件,求解二元一次非线性方程组。
查阅相关资料得到数据如下:
d=1.10km,l=1.36km,s=√(l^2-d^2 )=√(1.36^2-1.10^2 )=0.80km,1m/s≤v_0≤3m/s,20km/h≤v≤40km/h。
取一个合理范围内的轮船速度值 ,取一合理范围内的水流速度值 ,代入上述已知数据,利用MATLAB软件求解方程组,得到当轮船航行方向与河岸方向夹角为 时,此时航行时间最短约为 。
【设计意图】问题6到7是模型求解的过程,该过程可以基本实现“数学运算”水平二在知识与技能方面的要求,即能够使用编程软件设计运算程序求解,有助于发展学生数学运算、数学建模的核心素养。
问题8:你能验证模型结果的合理性吗?
可采用方式:查阅资料、应用地图软件、亲身实践。
【设计意图】探究既是5E教学模式的中心环节,又作为主线贯穿始终。通过这个环节可以基本实现“数学建模”水平二的要求,即学生能够在教师的引导下经历数学建模的完整过程,掌握数学建模的基本方法和步骤。该环节有助于提高学生的数学运算能力,提升学生的逻辑推理、数学建模的核心素养。
5.3 解释
问题9:请根据活动过程总结得出数学建模的一般步骤。
数学建模活动的一般步骤主要包括在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题(见图3)。

图3.数学建模一般步骤流程图
【设计意图】解释是5E教学模式的关键环节。该环节有助于帮助学生形成数学建模的概念,理解数学建模的基本思路与方法,发展学生数学建模核心素养。
5.4 精致
问题10:若进一步考虑水流速度的变化,对模型及结果有何影响?
水流速度并非定值,在两岸边和江面中央时速度显然不同,因此可将水流速度看为三段分布,在此基础上对模型进行改进。
问题11:若同时考虑水流速度和航行方向的变化,对模型及结果有何影响?
资料:自然界中的流体具有黏滞性,由牛顿黏性定律以及河岸的阻碍作用可知,江面中央的水流速度最快,而越靠近岸边水流速度越慢,并且江水流速近似与距岸边距离的平方成正比[5]。因此可将水速看为二次函数分布,通过计算机软件可得到水速和航向之间的关系,在此基础上改进模型。
问题12:通过对不同模型结果进行对比,你能得出什么结论?
数学模型没有对错没有最好,可以通过考虑更多的因素不断地优化模型,使之更加贴合实际情况。
【设计意图】精致是5E教学的拓展提升环节,该环节可针对不同层次的学生进行差异性教学,对学习能力较差的学生,讲解答疑,引导其对该问题进行回顾、理解和总结;对学有余力的同学,引导其在遵循客观规律的前提下,考虑现实情况进一步优化,调动批判性思维、创造性思维,提升逻辑推理能力,旨在更进一步地促进数学建模核心素养的发展。
5.5 评价
问题13:对已有模型的优缺点进行评价,并思考在条件允许的情况下,如何进一步优化改进模型。
问题14:谈谈本节课的收获,用自己的语言描述什么是数学建模,数学建模的过程如何,数学建模相比于常规课堂有哪些特点等。
问题15:“轮船渡江”模型可以用来解决大量有关两个矢量合成的问题,思考还有哪些可应用迁移的场景。
【设计意图】评价是5E教学模式的巩固提升环节。该环节学生通过小组交流、汇报分享等形式回顾本节课的过程,在与教师和同伴交流互动的过程中,不断反思并思考如何改进,有助于培养学生及时总结、深入思考的习惯,发展数学建模核心素养。
6 总结
本教学设计结合数学建模活动的特点,按照发展学生数学核心素养的目标设计教学过程,在教学目标中突出核心素养,在教学过程中落实核心素养,旨在通过完整的数学建模活动,培养学生达到数学建模水平二、数学运算水平二、数学抽象水平三的要求。
本设计基于5E教学模式的基本环节展开:引入环节,从现实情境中提出数学建模问题,对于激发学生的探究兴趣至关重要;探究环节,引导学生完成数学建模的核心步骤,经历数学建模的完整过程,掌握数学建模的基本方法,有助于发展学生的数学运算、数学抽象和数学建模的核心素养;解释环节,帮助学生形成数学建模的概念,理解数学建模的基本思路,提高学生归纳和概括的能力;精致环节,考虑更多因素优化,提升学生批判性思维、创造性思维;评价环节,浅谈收获的同时,发现不足并反思,培养学生及时总结、深入思考的习惯。
总的来看,5E教学模式本质是一种探究模式,学生数学核心素养的发展最主要在探究环节落实,在其他环节教师也应当尽可能地提升学生各方面的综合能力。
参考文献
[2] 任文韬. 基于5E教学模式的模型构建教学——以“种群数量的变化”为例[J]. 中学生物学,2019,35(08):26-28.
[3] 李红. 小船渡河 向量领航[J]. 新世纪智能,2019(93):35-36.
[4] 喻平. 核心素养指向的数学教学目标设计[J]. 数学通报,2021,60(11):1-5+13.
[5] 孟勇. 小船渡河问题的拓展[J]. 物理与工程,2022,32(03):95-99


