基于E-PBL教学模式的实数教学设计——以有理数加法为例

基于E-PBL教学模式的实数教学设计——以有理数加法为例

刘陈三

深圳明德实验学校（集团），深圳市，广东省，中国

摘要：本文应用E-PBL（Environment-Problem/Project/Play based Learning）教学模式对七年级数学“有理数加法”进行教学设计。通过创设贴近生活的情境，以问题为导向，结合现代信息技术手段，引导学生主动探究有理数加法的法则，培养学生的自主学习能力和问题解决能力，激发学生对数学学习的兴趣。

1 引言

实数内容的教学是初中数学中的重要内容，是计算的基础所在，而对于此类内容的日常教学往往会不太注重运算法则背后的逻辑与原理，多追求法则结果导致课堂比较枯燥。本文选取2024版北师大新教材七年级上册《有理数的加法·第1课时》为例，尝试运用E-PBL教学模式探讨课堂设计。它不仅要求学生掌握基本的加法运算，还要求学生理解加法法则背后的逻辑和原理。传统的讲授式教学往往使学生处于被动接受的状态，缺乏主动探索和思考的机会。而E-PBL教学模式强调以问题为中心，以活动为中心，以项目式教学[1]为中心，通过信息技术的辅助，创设丰富的学习情境，鼓励学生自主探究，从而提高学习效果。

我校数字教育生态支撑的创新教学体系（E-PBL）框架如图1所示，是指在数字化的时代下，如何有效运用技术手段，创设基于问题、项目和活动的学习模式，并配套对应的课堂教学评价量规。其中E（Environment）表示融合技术、平台、空间、资源的“互联网+教育”大环境；P具有三种解释：Problem（问题）是指以问题驱动学习，推动学习；Project（项目）指以设计并完成项目的方式开展教学；Play（活动）指以游戏、比赛、剧本等多种形式开展教学活动的方式；B（based）基于，L（learning）以学习为中心。

本教学流程设计采用以终为始的方式设计教学内容，具体包含确定教学目标、匹配评价方案、组织学习任务及教学策略、基于E-PBL生成教学过程四个部分。

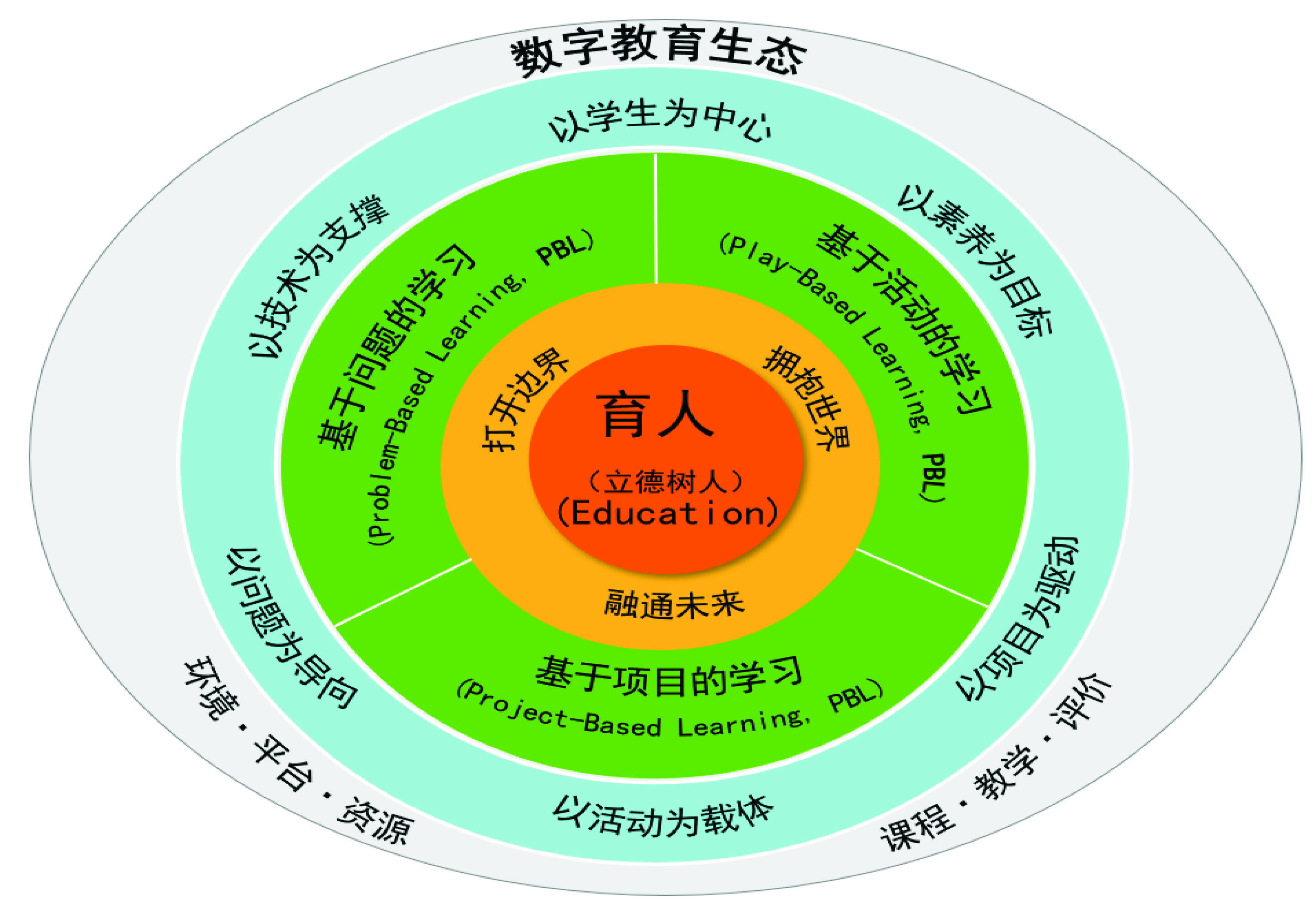
图1. 数字教育生态支撑的E-PBL教学创新体系框架

2 确定教学目标

2.1 教材分析

本节课是北师大新版教材七年级上册第二章第二节第一课时，是在数域扩充到负数后衔接小学阶段加法运算的第一次课。本节课前学习过相反数、绝对值、数轴。有理数的加法是建立在学生已经学习过有理数的相关概念之后进行的深入学习，也是有理数计算的开始以及有理数混合运算的基础。

2.2 学情分析

思维特点：从智力与能力发展的年龄特征看，七年级学生的思维正处于从以具体形象思维成分为主向抽象思维成分为主的转折期，因此，在探究有理数的加法法则时，创设的问题情境要注意具体性、形象性，同时还要有适当的抽象、概括要求。

认知水平：（1）学生在小学时已经有了深厚的计算功底，学生已经具备了计算的相应水平和能力。而在初中阶段则是进行进一步的学习和深入对有理数的计算进行学习，充满了信心。（2）学生具备初步的观察、分析和概括能力。有理数的运算是数式运算的基础，而有理数的加法是进一步学习有理数减法、乘法的基础，其中蕴含的思想方法对后续学习有积极的借鉴和引导作用。（3）明德实验学校校园环境有海豚元素及学生培养体系中有海豚银行体系，学生对此兴趣浓厚。

2.3 教学目标

依据课程标准[2]和教材要求[3]及学生现状，确定本节课的教学目标如下。

2.3.1 知识与技能

理解有理数加法法则；能利用加法法则进行简单的有理数加法运算。

通过探索有理数加法法则的过程，培养学生的数学抽象能力，使其能够从具体情境中抽象出数学规律和模型。

通过运算实践，发展学生的逻辑推理能力，使其能够基于法则进行正确的数学推导和判断。

2.3.2 过程与方法

采用启发式和探究式学习方式[4]，经历探索有理数加法法则的完整过程。

培养观察、比较、猜想、归纳、反思等能力，提升问题解决的能力。

渗透分类、数形结合、类比、从特殊到一般的数学思想方法，加深对数学本质的理解。

发展学生的直观想象能力，使其能够利用图形、图像等手段辅助理解和解决数学问题。

强化数学运算能力，确保学生在掌握有理数加法法则的基础上，能够熟练、准确地进行运算。

2.3.3 情感态度与价值观

借助现实情境理解加法法则，激发学生的学习兴趣，增强学习数学的内在动力[5]。

培养学生关注生活中的数学问题，提高将实际问题转化为数学问题的能力，即数学建模能力。

通过数据分析的过程，让学生体会到数学在解决实际问题中的价值，培养科学态度和探究精神。

2.4 教学重难点

教学重点：有理数加法法则的理解和应用。

教学难点：异号两数相加时符号的确定以及和的绝对值的计算。

3 匹配评价方案

根据教学目标，设计相应的评价方案，包括过程性评价和结果性评价。过程性评价主要关注学生在探究过程中的表现，如参与度、合作能力、思维能力等；结果性评价则通过课堂小测、作业等形式检验学生对有理数加法法则的掌握情况。

4 组织学习任务及教学策略

4.1 学习任务

依据前面评价方案，由易至难，制定梯度性的三个学习任务。

任务1：观察生活中的加减法现象，理解有理数加法的实际意义；

任务2：通过小组合作，探究有理数加法的法则；

任务3：利用有理数加法法则解决实际问题。

4.2 教学策略

情境导入：通过创设海豚商店中秋节活动的情境，引出有理数加法的实际问题；

问题探究：引导学生提出问题，如“如何计算海豚商店的总进货量和出货量？”等，并通过小组合作进行探究；

信息技术辅助：利用希沃平台等现代信息技术手段，展示数轴、动态演示等，帮助学生直观理解有理数加法的法则；

反馈与调整：根据学生在探究过程中的表现，及时调整教学策略，确保教学目标的达成。

5 基于E-PBL生成教学流程

5.1 设计思路

本次教学以E-PBL教学模式为指导，结合现代信息技术手段，创设贴近生活的情境，引导学生通过问题探究的方式学习有理数加法法则。具体设计思路如下：

Step 1：情境导入（5分钟）

通过海豚商店中秋节活动的情境，引出有理数加法的实际问题。

Step 2：问题探究（20分钟）

学生分组提出问题，并尝试利用数轴等工具进行探究；

教师巡回指导，鼓励学生交流讨论。

Step 3：法则总结（10分钟）

学生代表分享探究成果，教师总结有理数加法的法则；

利用信息技术手段展示动态演示，加深学生理解。

Step 4：应用练习（10分钟）

学生利用有理数加法法则解决实际问题；

教师及时反馈，纠正错误。

Step 5：课堂小结（5分钟）

回顾本节课的学习内容，强调有理数加法法则的重要性；

布置课后作业，巩固所学知识。

5.2 具体教学环节

【环节一】引入，探究同号相加

【导语】教师口述，中秋节前夕，小海豚向海豚银行贷款320元海豚币进货月饼开设海豚商店。下面（如图2）是小海豚中秋节前这几天的部分进出货数量。

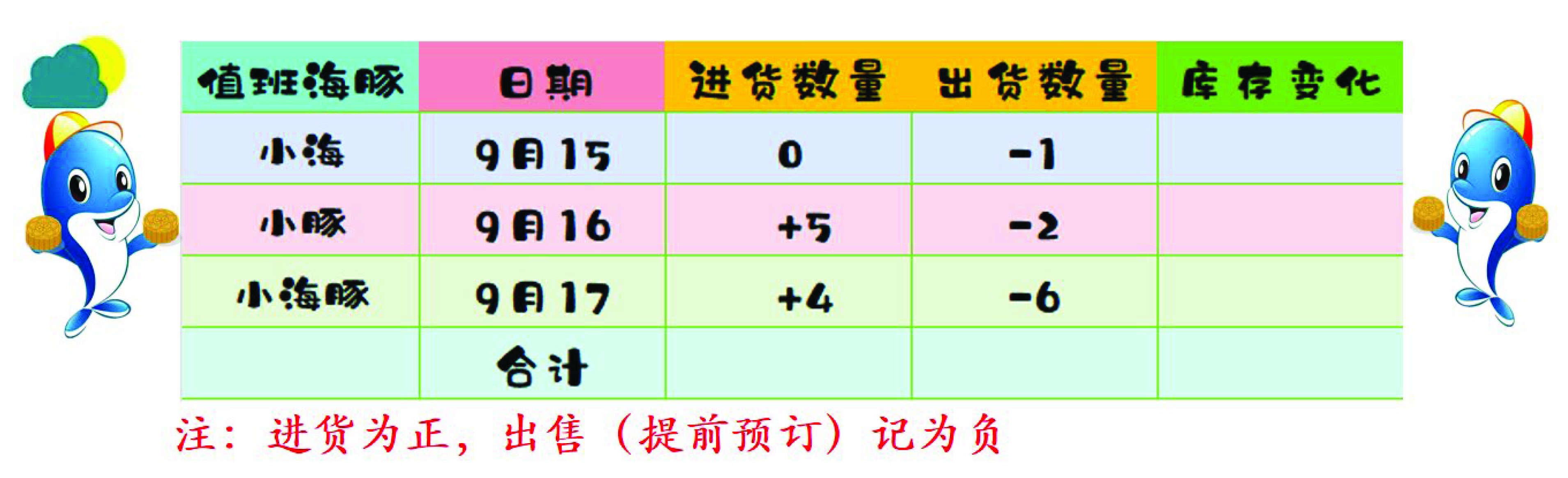
图2. 引入情境

请问：①9月16,17日共进货数量可以怎样列式？

②9月16,17日共出货数量可以怎样列式？

预设生成算式：（+5）+（+4）和（-2）+（-6）

以此铺垫进入环节一探究新知（一）（如图3）：结合小学加法的知识储备借助数轴建立模型理解（+5）+（+4）=+9，从而让学生类比探究理解：（-2）+（-6）=-8。

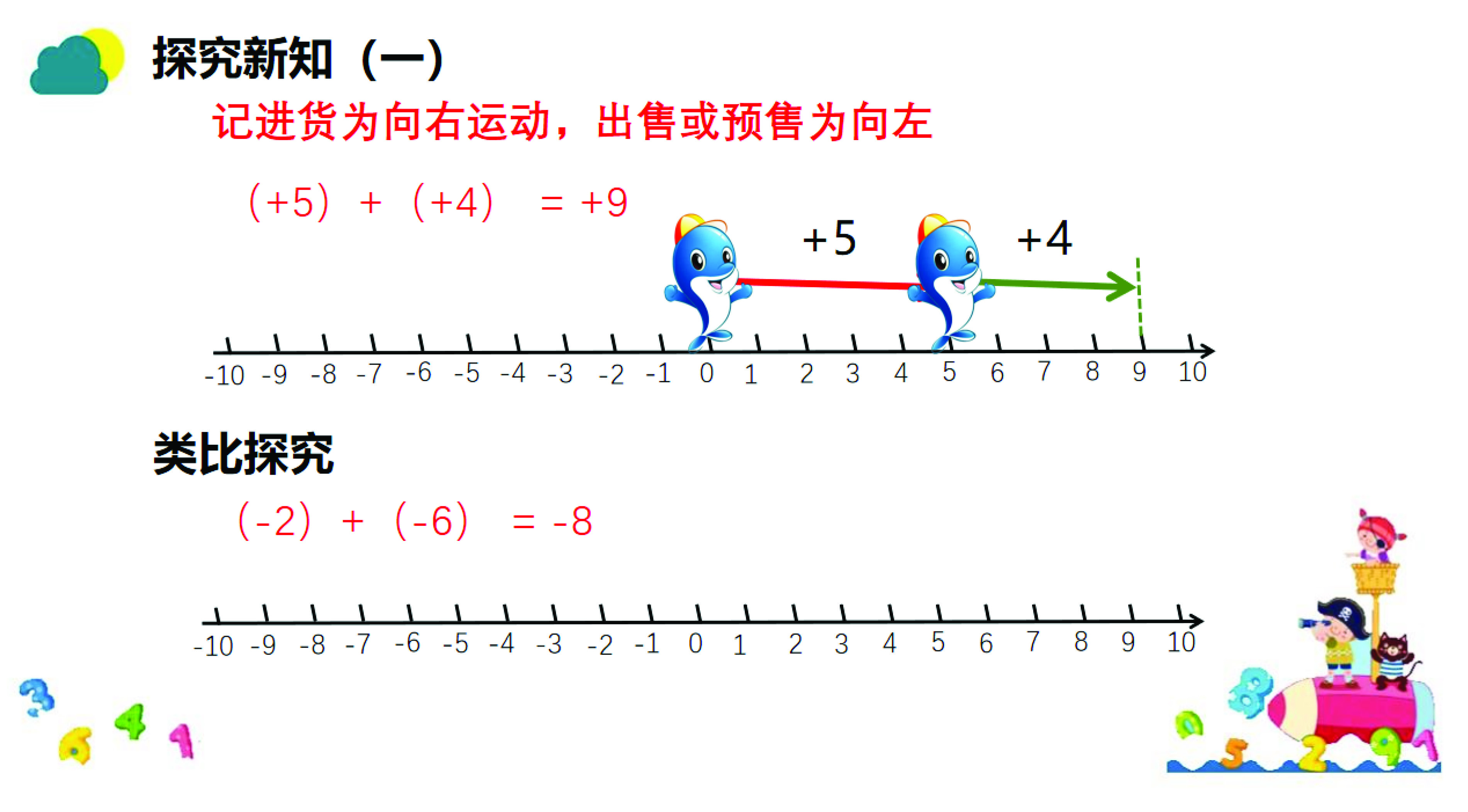
图3. 探究新知一

引导学生观察两个等式，进而提出问题③：观察两式的符号和绝对值，你能发现什么？

从而由学生生成同号相加的运算法则。

【指导性练习】教师利用一道例题引导规范书写，强化确定符号意识和绝对值相加的意识。由学生练习2-3道题。

【环节二】探究异号相加

提问④：小学阶段学习过哪些两项式加法类型？

提问⑤：学习负数后，又会产生哪些两项式加法类型？

小组合作：请根据海豚商店账单组内提问并列式（列式须区别于前述两式），从而生成：0+（-1），（+5）+（-2），（+4）+（-6）等类型的算式，结合已有的（+5）+（+4）= -9，（-2）+（-6）= -8丰富完善了加法的运算类型。

提问⑥：上述加法算式可以如何归类？

进而选取异号相加的两个算式设计探究活动二（如图4）：小组合作：同桌两人分别选取其中一个式子利用数轴计算，并向同桌分享。

图4. 探究新知二

在经历小组活动后，引到学生观察由学生生成的两个等式，并提问⑦：观察两式的符号和绝对值，你能发现什么？从而生成异号相加的法则。

为了突破本节课难点，此处围绕异号相加设计希沃白板的小游戏（图5），小组竞争的形式上台互动。突出符号判定以及绝对值的相加或相减运算。

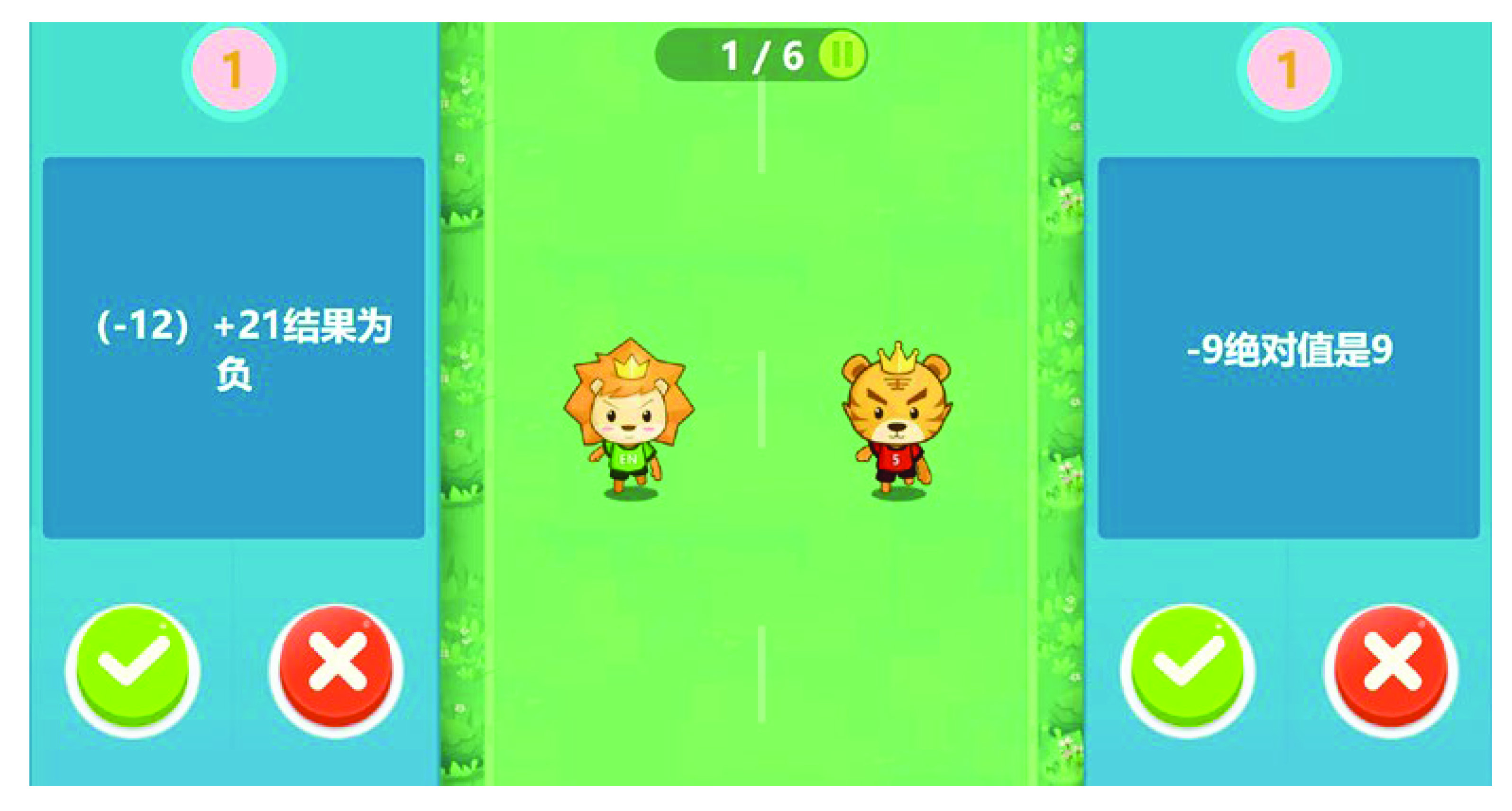
图5. 游戏互动

【环节三】结合前面已经历过的运算，优化海豚账单后继续提问：根据图示（图6）海豚商店账本，你还可以进行哪些提问和列式？

生成0+（+9），0+（-1），（+9）+（-9）等算式，从而生成0+一个数的情形和互为相反数相加的情形的运算法则。此类型学生容易理解，可以结合课堂学生反应情况对利用数轴理解法则环节取舍。

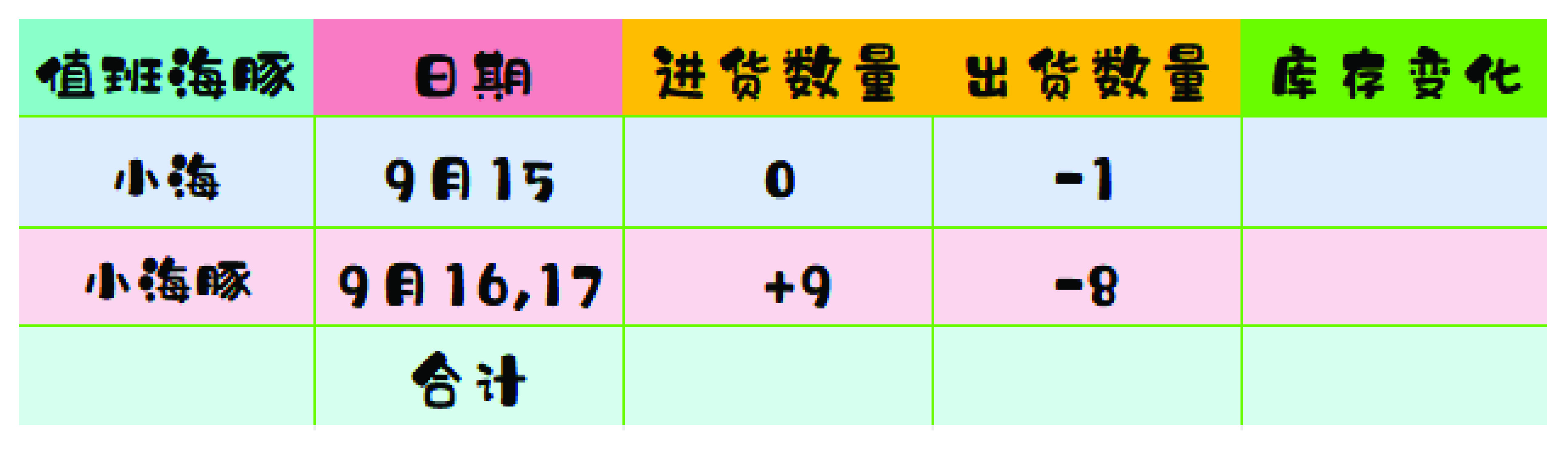
图6. 环节三

【环节四】课堂限时训练。设置6道左右训练题，巩固学生对相应运算类型的运算法则的理解。

【师生总结】：有理数加法运算形式有哪些？相应运算类型的法则是什么？你还有什么困惑？

5.7 分层作业布置

必做：B本第二章第二节第1课时P12-13

选做：学案第7题，B本P13面素养提升创新练第15题。

6 总结

本设计以E-PBL教学模式为指导，通过创设贴近生活的情境，引导学生主动探究有理数加法的法则，培养了学生的自主学习能力和问题解决能力。同时，结合现代信息技术手段，使教学过程更加生动有趣，激发了学生的学习兴趣。在未来的教学中，我们将继续探索和完善E-PBL教学模式的应用，为学生的学习提供更加有力的支持。

致谢

感谢广东省深圳市福田区教师发展中心举办的2024 年福田区“大先生”培养计划-“启航工程”。

感谢我校数学科组徐浩、王瑞、李德如等老师为本设计提供的修改建议和意见。

感谢我校E-PBL研究团队付华敏等老师提供的帮助。